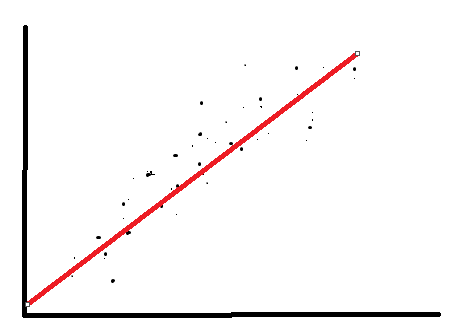
우리는 여러 자연현상이나 사회현상들을 보고 궁금증이 생길 때가 많다.
왜 저건 저렇게 될까?
아마 원인과 결과가 있을 것이고 우리는 이와 같은 현상들을 이해하고 규명하고자 여러가지 방법들을 제시하고 있다.
특히 어떤 현상이 변수들의 인과관계에 의하여 나타날 때 그 관계를 수학적으로 설명하기 위해서 사용되는 통계적 방법들 중 하나가 회귀분석(Regression analysis)이다.
# 회귀식이란?
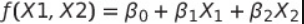
위의 식등의 수학적 모형을 회귀식(regression equation)이라 한다.

# 회귀계수(regression coefficient)

위와 같이 베타종류를 설명변수와의 관계를 설명하는 계수로 활용해 회귀계수라고 부른다.
회귀식을 추정한다는 것은 곧 회귀계수들의 값을 추정하는 것이 되는데 베타의 크기에 따라서 상관관계를 설명할 수 있기 때문이다.
회귀계수가 0이 되는것은 독립변수와 반응변수와의 관계가 없다. 독립적이다. 라고 설명할 수 있다.
회귀분석은 '회귀계수에 대한 분석'이라고 생각하면 좋다.
# 회귀분석을 하는 목적
일반적으로 회귀분석을 하는 목적을 다음과 같이 말할 수 있다.
(1) 변수들 간에 성립하는 정확한 회귀모형의 구축(model building)
(2) 모형에 포함된 모수들의 추정(parameter estimation)
(3) 적합된 모형을 이용한 예측(prediction)
그런데 회귀분석을 하는 과정에서 회귀모형은 분석의 목적이나 방향에 따라 다를 수 있다.
예를 들면, 모형의 구축(postulated)이 주 목적이면 통계적으로 유의미한 내용이 나타나지 않은 경우에도 해당 설명변수를 분석자가 중요하다고 판단하면 모형에 포함시킬 수 있다.
따라서 사전에 자료분석의 목적을 정확히 정의하는 일과 그에 맞는 통계량과 분석방법을 정하는 것은 매우 중요하다.
'수학&통계학 > 회귀분석' 카테고리의 다른 글
| 가변수를 이용한 회귀분석 (0) | 2023.04.07 |
|---|---|
| 표준화 잔차 (standarized residual) (0) | 2023.04.06 |
| 최소제곱법은 왜 쓸까? (0) | 2022.11.05 |
| 오차항(error) vs 잔차(residual) (0) | 2022.11.05 |



댓글